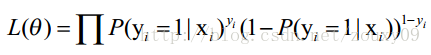多元回归方程:假设有一个因变量y和一组自变量x1, x2, x3, ... , xn,其中y为连续变量,我们可以拟合一个线性方程:
y =β0 +β1*x1 +β2*x2 +β3*x3 +...+βn*xn
如果y为二分类变量,只能取值0或1,那么线性回归方程就会遇到困难: 方程右侧是一个连续的值,取值为负无穷到正无穷,而左侧只能取值[0,1],无法对应。为了继续使用线性回归的思想,统计学家想到了一个变换方法,就是将方程右边的取值变换为[0,1]。最后选中了Logistic函数:逻辑回归,可以说是在线性回归的基础上加上一个sigmoid函数,将线性回归产生的值归一化到[0-1]区间内。sigmoid函数如下:
y = 1 / (1+e-x)
这是一个S型函数,值域为(0,1),能将任何数值映射到(0,1),且具有无限阶可导等优良数学性质。
我们将线性回归方程改写为:
y = 1 / (1+e-z),
其中,z =β0 +β1*x1 +β2*x2 +β3*x3 +...+βn*xn
此时方程两边的取值都在0和1之间。
进一步数学变换,也就是可以写为:
Ln(y/(1-y)) =β0 +β1*x1 +β2*x2 +β3*x3 +...+βn*xn
Ln(y/(1-y))称为Logit变换。我们再将y视为y取值为1的概率p(y=1),因此,1-y就是y取值为0的概率p(y=0),所以上式改写为:
p(y=1) = ez/(1+ez),
p(y=0) = 1/(1+ez),
其中,z =β0 +β1*x1 +β2*x2 +β3*x3 +...+βn*xn.
(你看吼,你需要估计某件事发生的概率,这时候你有大量的训练样本,所以你想用一个多元回归来估计这个事儿,但是你多元回归所算出来的值特别多,而你的概率只处于0和1之间,这时候吧你就需要logistics了,)
接下来就可以使用”最大似然法”估计出各个系数β。
本文基本借鉴:http://blog.sina.com.cn/s/blog_44befaf60102vznn.html
这个出自:http://blog.csdn.net/YoYoDelphine/article/details/52888276
(你看吼,你所估计的跟真实值肯定有出入吧,这时候就需要找最优化的各个系数β吧,那你怎么找呢,就需要一个代价函数,代价函数分很多,求参有多种方法。比如最小二乘,比如最大然,比如交叉熵,这里用极大然是为了使这件事发生的概率最大化,也就是已知x,求β)
所谓参数估计就是:对未知参数θ进行估计时,在参数可能的取值范围内选取,使“样本获得此观测值x1,x2...,xn”的概率最大的参数θ^作为θ的估计,这样选定的θ^有利于x1,x2...,xn”的出现。也就是说在已知数据集(结果)和模型(分布函数)的情况下,估计出最适合该模型的参数。
举个例子:
假设你有一枚硬币,随机抛10次;现在的结果是6次正面。我们都知道,抛一枚硬币,正面朝上和反面朝上的概率均是θ=0.5;但前提时,这是在大量的实验(抛硬币)情况下才有的结论。那在我们这个情况下,参数θ到底取何值时才能使得出现6次正面的肯能性最大呢?
详情参见:http://blog.csdn.net/The_lastest/article/details/78761577

也就是n个独立的样本出现的似然函数为(因为每个样本都是独立的,所以n个样本出现的概率就是他们各自出现的概率相乘):
那最大似然法就是求模型中使得似然函数最大的系数取值θ*。这个最大似然就是我们的代价函数(cost function)了。
(截自李航《统计学习方法》)
(你看吼,这时候带代价函数,这里的代价函数就是这个事儿所有属性发生的概率*不发生的概率,就需要求β,然后需要用到梯度下降法对于每次的β迭代,也就是求导,对于极大似然函数求导,导数的方向也就是最好的下降方向 ,然后我们令该导数为0,你会很失望的发现,它无法解析求解。不信你就去尝试一下。所以没办法了,只能借助高大上的迭代来搞定了。这里选用了经典的梯度下降算法。
)
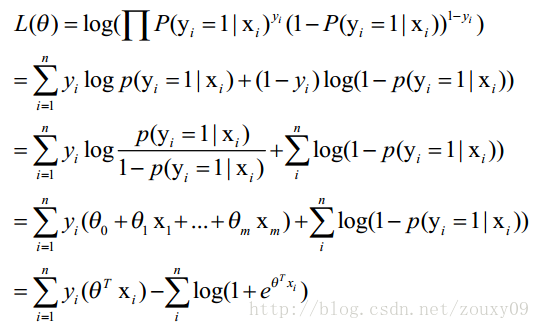
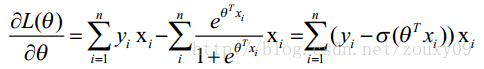
(θ求完导之后发现是θ=θ1+步长*(错误率)*本来的xi,下面就是优化了,在样本容量非常大的时候,你要随机选则,节省时间,然后就是逐步减小步长,这个在牛顿法中可以理解,迭代次数越高,越合适)
代码参考:http://blog.csdn.net/zouxy09/article/details/20319673
本文仅作作者笔记,没有任何冒犯的意思。。。